The reasons people have for getting itchy and upset over a word changing meaning are many and varied. For some, umbrage accompanies any form of semantic drift, while others choose to complain only when they fear that some specific word is in danger of losing its specificity. Specialists in technical fields seem to be particularly fond of inveighing against a word taking a new meaning; a recent trend we have observed is the mathematically inclined arguing against the broadened use of exponential.
"Exponential Growth" and "Doubling Times" are much more than "buzzwords." They are specific well-defined mathematical terms, as was set forth in careful detail in the Paper's first listed reference, Bartlett (1993).
— Albert A. Bartlett, Population and Environment, Sept. 2003Is your understanding of these terms growing exponentially? No! thunders a tonality of mathematicians. “I’m vexed to hear some trend described as ‘growing exponentially’ when the writer means it is growing rapidly,” writes Maurice Fox of Arlington, Va.
— William Safire, The New York Times, 6 May 2001Alas, some recent hits reveal that the word is often used just to mean “lots.” Tasks are “exponentially more difficult” if one is blind, space war “exponentially more dangerous” than that on earth.
— Manil Suri, The New York Times, 4 Mar. 2019
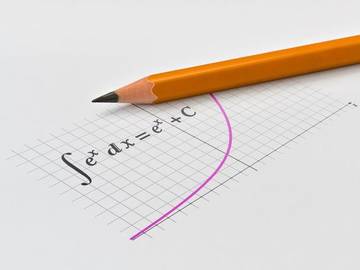
Please do not ask us to explain this math.
An exponent is “a symbol written above and to the right of a mathematical expression to indicate the operation of raising to a power,” and the mathematical senses of exponential include “of or relating to an exponent” and “involving a variable in an exponent.” These senses are appropriately mathy, and if the word had simply stopped there all would be well in the world.
But exponential also took on the meaning “expressible or approximately expressible by an exponential function; especially : characterized by or being an extremely rapid increase (as in size or extent).” It’s this ‘approximately expressible’ sense, especially the part that comes after the word especially in the above definition, that irks those aficionados of specificity, who very much desire that exponential not end up simply functioning as a synonym of lots. Given that we, and several other lexicographic concerns, define exponential in this "not what your math teacher means" way, it seems worth asking: why do lexicographers hate math?
We don’t, but even if we did, that wouldn’t be why we define exponential like this. We define words the way that they are used, and it is important to acknowledge that it is we who follow the lead of speakers of our language, and not the other way around. By the time we get around to entering and defining words it is because they have already arrived, not because we want to introduce them. Lexicographers do not give a seal of approval, they merely catalogue what has already been approved of by the people who use the language.
We do not think you need to worry that the new-fangled sense of exponential will blunt the precision of the strict mathematical sense. There are plenty of words in English which hold a precise application in one field, and a broader range of meanings in general use. As a means of demonstrating this, we have here a short quiz, with three common terms from math: calculus, angle, and multiply. See if you can distinguish between the math-related sense and the general use in each of the following pairs of citations.
Calculus
The Saudi leader's excursion into Asia offered a close-up view of how that is altering the political calculus for other countries.
— New Temko, The Christian Science Monitor (Boston, MA), 26 Feb. 2019Basic integral calculus teaches that certain indefinite integrals have no closed form, but sadly most students never learn why.
— D. V. Feldman, Choice, Nov. 2015
Angle
”Get away with that publicity stuff, what’s your angle?” a listener countered.
— Kansas City Star (Kansas City, MO), 22 Feb. 1923It should be noted that we now have applied the word corresponding to certain angles of congruent figures and to certain angles formed when a transversal cuts two other lines, which will almost invariably be two parallel lines.
— Herbert E. Hawkes & William A. Luby, Plane geometry, 1920
Multiply
As we grow in years our work grows, our problems multiply, and take on difference shapes in the different territory included in Boston.
— The Boston Globe, 11 Nov. 1892Suppose you would multiply 7 by 8, find the 8 at the Top, and the 7 in the Side, and in the Square where they meet stands 56 the Product, and so of any other.
— Richard Carr, The young arithmetician and algebraist’s companion, 1751
Perhaps the mathematicians will now ask ‘how would you feel if people started using the word dictionary to mean anything other than “a reference source in print or electronic form containing words usually alphabetically arranged along with information about their forms, pronunciations, functions, etymologies, meanings, and syntactic and idiomatic uses”? What if people started using lexicographer with the meaning of “killjoy”?’
We can tell you the answer to at least one of these questions, as people have been using dictionary in an extended sense for some while, and so we provide a number of definitions for the word. In addition to describing the alphabetized list of words, a dictionary may also refer to “a general comprehensive list, collection, or repository,” “a list (as of data items or words) stored in a computer for reference (as for information retrieval or word processing),” and several other things besides.
And if you can convince enough people to use the word lexicographer as a synonym for killjoy, rest assured we will add that as a definition. Furthermore, we will do so without complaining that some sacrosanct specificity of language has been lost.




